Note: les tables de vérité ci-dessous sont transposées par rapport
aux tables de vérité des pages précédentes, les rangées
sont devenues des colonnes et vice-versa.
| logique
| tétravalente
| binaire
|
| Valeurs élémentaires
| T, F, B, N
{} dénote l'absence de valeur
| 1, 0
pas de concept d'absence de valeur
|
| diagramme de Venn
| Le diagramme au complet représente l'ensemble de toutes les assertions possibles en logique tétravalente.
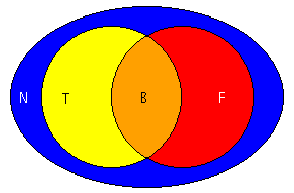
- rond jaune
- l'ensemble 1 des assertions vraies: 1 = T|B
- rond rouge
- l'ensemble 0 des assertions fausses: 0 = F|B
- zone orange
- l'ensemble B des assertions vraies-et-fausses: B = 1&0
- zone bleue
- l'ensemble N des assertions ni-vraies-ni-fausses: N = ¬(1|0)
| Le diagramme au complet représente l'ensemble de toutes les assertions possibles en logique binaire.
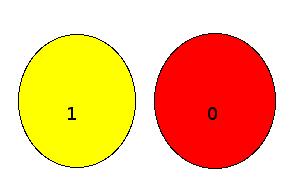
- rond jaune
- l'ensemble 1 des assertions vraies
- rond rouge
- l'ensemble 0 des assertions fausses
- milieu exclu
- on voit que les ensembles 1 et 0 sont disjoints
- tiers exclu
- on voit qu'il n'existe pas d'assertion en dehors des ensembles 1 et 0
|
| opérateur unaire
| ¬ complément
| X | ¬X
| | T | ¬T = F|B|N
| | F | ¬F = T|B|N
| | B | ¬B = T|F|N
| | N | ¬N = T|B|F
|
|
|
| X | ¬X
| | 1 = T|B | ¬1 = F|N
| | 0 = F|B | ¬0 = T|N
|
|
| ¬ négation
|
| & intersection, conjonction (et)
| (X & Y)
| X Y
| T | F
| B | N
| | T | T | {} | {} | {}
| | F | {} | F | {} | {}
| | B | {} | {} | B | {}
| | N | {} | {} | {} | N
|
|
|
|
| (X & Y)
|
| | union, disjonction (ou)
| (X | Y)
| X Y
| T | F
| B | N
| | T | T | T|F | 1 | ¬0
| | F | T|F | F | 0 | ¬1
| | B | 1 | 0 | B | B|N
| | N | ¬0 | ¬1 | B|N | N
|
|
|
|
| (X | Y)
|
| - différence (sauf)
| (X - Y) signifie (X & ¬Y)
| X Y
| T | F
| B | N
| | T | {} | T | T | T
| | F | F | {} | F | F
| | B | B | B | {} | B
| | N | N | N | N | {}
|
|
|
|
| (X - Y) signifie (X & ¬Y)
|
| % exclusion (ou exclusif)
| (X % Y) signifie ( (X & ¬Y) | (Y & ¬X) )
| X Y
| T | F
| B | N
| | T | {} | T|F | 1 | ¬0
| | F | T|F | {} | 0 | ¬1
| | B | 1 | 0 | {} | B|N
| | N | ¬0 | ¬1 | B|N | {}
|
|
|
|
| (X % Y) signifie ( (X & ¬Y) | (Y & ¬X) )
|
| équivalence
| = égalité et \ inégalité
(X = Y) signifie SI tout élément de X est un élément de Y et tout élément de Y est un élément de X ALORS T SINON F
| X Y
| T | F
| B | N
| | T | T | F | F | F
| | F | F | T | F | F
| | B | F | F | T | F
| | N | F | F | F | T
|
|
|
inégalité :
(X \ Y) = ( (X = Y) = F )
|
| <=> bi-implication
(X <=> Y) signifie ( (X & Y) | (¬X & ¬Y) )
|
| < appartenance
| (X < Y) signifie ( (X & Y) = X )
| X Y
| T | F
| B | N
| | T | T | F | F | F
| | F | F | T | F | F
| | B | F | F | T | F
| | N | F | F | F | T
|
|
|
( (X | Y) < Z ) = ( (X < Z) & (Y < Z) )
( X < (Y & Z) ) = ( (X < Y) & (X < Z) )
|
| (X < Y) signifie ( (X & Y) <=> X )
|
| > inclusion
| (X > Y) signifie (Y < X)
| (X > Y) signifie (Y < X)
|
| -> implication
| (X -> Y) signifie SI (X < T) ALORS Y SINON
SI (X < B) ALORS postposer la résolution SINON RIEN
| X Y
| T | F
| B | N
| | T | T | F | B | N
| | F | {} | {} | {} | {}
| | B | B -> T | B -> F
| B -> B | B -> N
| | N | {} | {} | {} | {}
|
|
|
|
| (X -> Y) signifie ( (X < 0) | (Y < 1) )
|
| <- condition
| (X <- Y) signifie (Y -> X)
| (X <- Y) signifie (Y -> X)
|

