Logique tétravalente
Symétrie et opérateur ¬ (complément)
Le concept même de négation n'ayant aucun sens en logique tétravalente,
l'opérateur négation y est remplacé par l'opérateur complément,
que l'on note par le signe "¬".
| Loi de fermeture:
|
| Pour tout ensemble p il existe un ensemble unique ¬p
appelé complément de p.
|
| ¬p est l'ensemble qui comprend tous les éléments
de TFBN sauf ceux de p.
|
|
|
| Loi d'involution:
|
| ¬(¬p) est identiquement égal à p.
|
| p est le complément de ¬p tout comme ¬p
est le complément de p.
|
|
|
| L'ensemble p et son complément ¬p sont disjoints
(c-à-d: ils n'ont aucun élément en commun).
|
| Table de vérité du complément:
|
|
| p | ¬p
| | TFBN | {} l'ensemble vide
| | T | FBN = (F ou B ou N)
| | F | TBN = (T ou B ou N)
| | B | TFN = (T ou F ou N)
| | N | TFB = (T ou F ou B)
| | vrai = TB | FN = (F ou N)
| | faux = FB | TN = (T ou N)
| | test = TF | BN = (B ou N)
|
|
|
| Le vrai et le faux en logique tétravalente:
| | vrai | =
| (T ou B) | =
| TB
| | faux | =
| (F ou B) | =
| FB
| | ¬vrai | =
| (F ou N) | =
| FN
| | ¬faux | =
| (T ou N) | =
| TN
| | (vrai et faux) | =
| (TB et FB) | =
| B
| | (vrai et ¬faux) | =
| (TB et TN) | =
| T
| | (¬vrai et faux) | =
| (FN et TB) | =
| F
| | (¬vrai et ¬faux) | =
| (FN et TN) | =
| N
|
|
Symétrie de la logique tétravalente
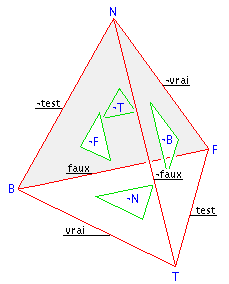
| On peut représenter les sous-ensembles de TFBN sous la forme de ce tétraèdre, ce qui
permet de visualiser les relations de symétrie dues à l'opérateur complément:
| le volume du tétraèdre représente l'univers logique:
|
|---|
| TFBN = (T ou F ou B ou N)
|
|
| les 4 sommets représentent les 4 singletons:
|
|---|
| T
| F
| B
| N
|
|
| les 6 arêtes représentent les 6 paires de valeurs:
|
|---|
| vrai = TB = (T ou B)
| faux = FB = (F ou B)
| test = TF = (T ou F)
| | ¬vrai = FN = (F ou N)
| ¬faux = TN = (T ou N)
| ¬test = BN = (B ou N)
|
|
| les 4 faces représentent les 4 triplets de valeurs:
|
|---|
| ¬T = FBN = (F ou B ou N)
| ¬F = TBN = (T ou B ou N)
| ¬B = TFN = (T ou F ou N)
| ¬N = TFB = (T ou F ou B)
|
|
| l'ensemble vide {} n'est pas représenté
|
|---|
|
|
On voit que chaque sous-ensemble de TFBN est situé exactement à l'opposé
de son complément dans le tétraèdre.
On voit aussi que la logique binaire usuelle ne correspond qu'aux deux sommets T et F
du tétraèdre, les deux sommets N et B y étant confondus avec le
sommet F. Pire encore, la logique binaire usuelle confond aussi l'ensemble vide {}
avec le sommet F. La perte d'information quand on ramène toute la logique à
la seule logique binaire usuelle est donc énorme.
Copyright © 2005-2008, Norman Molhant
Droit de copie et de diffusion accordés gratuitement à deux conditions:
1. ne pas altérer ni retirer la mention du copyright avec ces conditions
2. offrir gratuitement la consultation et le téléchargement de cette page